PENGERTIAN MATRIKS
Matriks adalah suatu susunan elemen-elemen atau entri-entri yang berbentuk persegipanjang yang diatur dalam baris dan kolom. Susunan elemen ini diletakkan dalam tanda kurung biasa ( ), atau kurung siku [ ]. Elemen-elemen atau entri-entri tersebut dapat berupa bilangan atau berupa huruf.
Matriks dinotasikan dengan huruf kapital seperti A, B, C dan seterusnya. Sedangkan elemennya, jika berupa huruf, maka ditulis dengan huruf kecil.
Dalam matriks A = [ aij ], dengan i dan j merupakan bilangan bulat yang menunjukkan baris ke-i dan kolom ke-j. Misalnya a12 artinya elemen baris ke-1 dan kolom ke-2.
Jenis - jenis Matriks
Matriks dapat dibedakan menurut jenisnya, antara lain:
a) Matriks Nol
Suatu matriks dikatakan sebagai matriks nol, jika semua elemennya sama dengan nol. Misalnya,
Semua unsur pada matriks A, B, dan C adalah angka 0, sehingga disebut sebagai matriks nol.
b) Matriks Baris
Suatu matriks dikatakan sebagai matriks baris, jika matriks tersebut hanya terdiri atas satu baris, misalnya
Suatu matriks dikatakan sebagai matriks baris, jika matriks tersebut hanya terdiri atas satu baris, misalnya
Matriks P berordo 1 × 3, Q berordo 1 × 2, dan R berordo 1 × 4. Matriks P, Q, dan R di atas hanya
memiliki satu baris saja sehingga disebut sebaai matriks baris.
c) Matriks Kolom
Suatu matriks dikatakan sebagai matriks kolom, jika matriks tersebut hanya terdiri dari satu kolom.
Suatu matriks dikatakan sebagai matriks kolom, jika matriks tersebut hanya terdiri dari satu kolom.
Misalnya,
Matriks K berordo 2 × 1, matriks L beordo 3 × 1, dan matriks M berordo 4 ×1. Matriks K, L, dan M di atas hanya memiliki satu kolom saja sehingga disebut sebagai matriks kolom.
d) Matriks Persegi atau Matriks Kuadrat
Suatu matriks dikatakan sebagai matriks persegi atau matriks kuadrat, jika jumlah baris pada matriks
Suatu matriks dikatakan sebagai matriks persegi atau matriks kuadrat, jika jumlah baris pada matriks
tersebut sama dengan jumlah kolomnya.Misalnya,
Matriks N berordo 2 × 2 dan matriks M berordo 3 × 3. Karena banyaknya baris sama dengan
banyaknya kolom, maka matriks N dan M disebut sebagai matriks persegi.
e) Matriks Segitiga
Suatu matriks persegi dikatakan sebagai matriks segitiga jika elemenelemen yang ada di bawah atau di
Suatu matriks persegi dikatakan sebagai matriks segitiga jika elemenelemen yang ada di bawah atau di
atas diagonal utamanya (salah satu, tidak kedua-duanya) bernilai nol. Jika elemen-elemen yang ada di
bawah diagonal utama bernilai nol maka disebut sebagai matriks segitiga atas. Sebaliknya, jika elemen-
elemen yang ada di atas diagonal utamanya bernilai nol maka disebut sebagai matriks segitiga bawah.
Misalnya,
f ) Matriks Diagonal
Suatu matriks persegi dikatakan sebagai matriks diagonal jika elemenelemen yang ada di bawah dan di
Suatu matriks persegi dikatakan sebagai matriks diagonal jika elemenelemen yang ada di bawah dan di
atas diagonal utamanya bernilai nol, atau dengan kata lain elemen-elemen selain diagonal utamanya bernilai
nol. Misalnya,
g) Matriks Skalar
Suatu matriks diagonal dikatakan sebagai matriks skalar jika semua elemen-elemen yang terletak pada
Suatu matriks diagonal dikatakan sebagai matriks skalar jika semua elemen-elemen yang terletak pada
diagonal utamanya memiliki nilai yang sama, misalnya
h) Matriks Identitas atau Matriks SatuanSuatu matriks skalar dikatakan sebagai matriks identitas jika semua elemen yang terletak pada diagonal
utamanya bernilai satu, sehingga matriks identitas disebut juga matriks satuan. Misalnya,






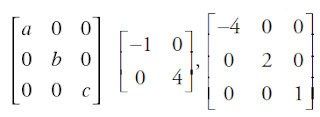


0 comments:
Post a Comment